Lecture 6, Heat transports

Two-dimensional advection-diffusion of heat

import xarray as xr
import numpy as np
import matplotlib.pyplot as plt

from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets

from IPython.display import HTML
from IPython.display import display

1) Background: two-dimensional advection-diffusion

1.1) The two-dimensional advection-diffusion equation

Recall from the last Lecture that the one-dimensional advection-diffusion equation is written as

\[\frac{\partial T(x,t)}{\partial t} = -U \frac{\partial T}{\partial x} + \kappa \frac{\partial^{2} T}{\partial x^{2}},\]

where \(T(x, t)\) is the temperature, \(U\) is a constant advective velocity and \(\kappa\) is the diffusivity.

The two-dimensional advection diffusion equation simply adds advection and diffusion operators acting in a second dimensions \(y\) (orthogonal to \(x\)).

\[\frac{\partial T(x,y,t)}{\partial t} = u(x,y) \frac{\partial T}{\partial x} + v(x,y) \frac{\partial T}{\partial y} + \kappa \left( \frac{\partial^{2} T}{\partial x^{2}} + \frac{\partial^{2} T}{\partial y^{2}} \right),\]

where \(\vec{u}(x,y) = (u, v) = u\,\mathbf{\hat{x}} + v\,\mathbf{\hat{y}}\) is a velocity vector field.

Throughout the rest of the Climate Modelling module, we will consider \(x\) to be the longitundinal direction (positive from west to east) and \(y\) to the be the latitudinal direction (positive from south to north).

1.2) Reminder: Multivariable shorthand notation

Conventionally, the two-dimensional advection-diffusion equation is written more succintly as

\[\frac{\partial T(x,y,t)}{\partial t} = - \vec{u} \cdot \nabla T + \kappa \nabla^{2} T,\]

using the following shorthand notation.

The gradient operator is defined as

\[\nabla \equiv (\frac{\partial}{\partial x}, \frac{\partial }{\partial y})\]

such that

\[\nabla T = (\frac{\partial T}{\partial x}, \frac{\partial T}{\partial y})\]

\[\vec{u} \cdot \nabla T = (u, v) \cdot (\frac{\partial T}{\partial x}, \frac{\partial T}{\partial y}) = u \frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}.\]

The Laplacian operator \(\nabla^{2}\) (sometimes denoted \(\Delta\)) is defined as

\[\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}\]

such that

\[\nabla^{2} T = \frac{\partial^{2} T}{\partial x^{2}} + \frac{\partial^{2} T}{\partial y^{2}}.\]

The divergence operator is defined as \(\nabla \cdot [\quad]\), such that

\[\nabla \cdot \vec{u} = \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial x} \right) \cdot (u,v) = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}.\]

Note: Since seawater is largely incompressible, we can approximate ocean currents as a non-divergent flow, with \(\nabla \cdot \vec{u} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0\). Among other implications, this allows us to write:

\begin{align} \vec{u} \cdot \nabla T&= u\frac{\partial T(x,y,t)}{\partial x} + v\frac{\partial T(x,y,t)}{\partial y}\newline &= u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + T\left(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}\right)\newline &= \left( u\frac{\partial T}{\partial x} + T\frac{\partial u}{\partial x} \right) + \left( v\frac{\partial T}{\partial y} + \frac{\partial v}{\partial y} \right) \newline &= \frac{\partial (uT)}{\partial x} + \frac{\partial (vT)}{\partial y}\newline &= \nabla \cdot (\vec{u}T) \end{align}

using the product rule (separately in both \(x\) and \(y\)).

This lets us finally re-write the two-dimensional advection-diffusion equation as:

\(\frac{\partial T}{\partial t} = - \nabla \cdot (\vec{u}T) + \kappa \nabla^{2} T\)

which is the form we will use in our numerical algorithm below.

2) Numerical implementation

2.1) Discretizing advection in two dimensions

In the last lecture we saw that in one dimension we can discretize a first-partial derivative in space using the centered finite difference

\[\frac{\partial T(x_{i}, t_{n})}{\partial x} \approx \frac{T_{i+1}^{n} - T_{i-1}^{n}}{2 \Delta x}.\]

In two dimensions, we discretize the partial derivative the exact same way, except that we also need to keep track of the cell index \(j\) in the \(y\) dimension:

\[\frac{\partial T(x_{i}, y_{j}, t_{n})}{\partial x} \approx \frac{T_{i+1,\, j}^{n} - T_{i-1,\,j}^{n}}{2 \Delta x}.\]

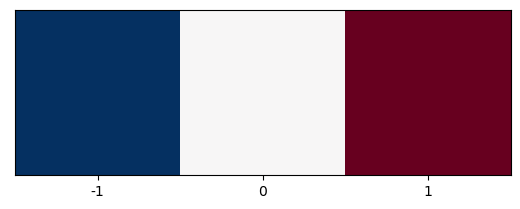
The x-gradient kernel below, is shown below, and is reminiscent of the edge-detection or sharpening kernels used in image processing and machine learning:

plt.imshow([[-1,0,1]], cmap=plt.cm.RdBu_r)
plt.xticks([0,1,2], labels=[-1,0,1]);
plt.yticks([]);

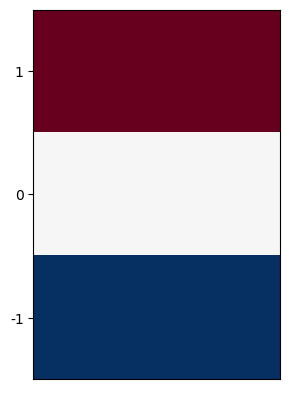
The first-order partial derivative in \(y\) is similarly discretized as:

\[\frac{\partial T(x_{i}, y_{j}, t_{n})}{\partial y} \approx \frac{T_{i,\, j+1}^{n} - T_{i,\,j-1}^{n}}{2 \Delta y}.\]

Its kernel is shown below.

plt.imshow([[-1,-1],[0,0],[1,1]], cmap=plt.cm.RdBu);
plt.xticks([]);
plt.yticks([0,1,2], labels=[1,0,-1]);

Now that we have discretized the two derivate terms, we can write out the advective tendency for computing \(T_{i, j, n+1}\) as

\[u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} \approx u_{i,\, j}^{n} \frac{T_{i,\, j+1}^{n} - T_{i,\,j-1}^{n}}{2 \Delta y} + v_{i,\, j}^{n} \frac{T_{i,\, j+1}^{n} - T_{i,\,j-1}^{n}}{2 \Delta y}.\]

We implement this as a the advect function. This computes the advective tendency for the \((i,j)\) grid cell.

xkernel = np.zeros((1,3))
xkernel[0, :] = np.array([-1,0,1])

ykernel = np.zeros((3,1))
ykernel[:, 0] = np.array([-1,0,1])

class OceanModel:
    
    def __init_(self,T, u, v, deltax, deltay):
        self.T = [T] 
        self.u = u
        self.v = v
        self.deltax = deltax
        self.deltay = deltay
        self.j = np.arange(0, self.T[0].shape[0])
        self.i = np.arange(0, self.T[0].shape[1])
        
    def advect(self, T):
        T_advect = np.zeros((self.j.size, self.i.size))
        
        for j in range(1, T_advect.shape[0] - 1):
            for i in range(1, T_advect.shape[1] - 1):
                T_advect[j, i] = -(self.u[j, i] * np.sum(xkernel[0, :] * T[j, i-1 : i + 2])/(2*self.deltax) +
                                   self.v[j, i] * np.sum(ykernel[:, 0] * T[j-1:j+2, i])/(2*self.deltay))
        return T_advect    

2.2) Discretizing diffusion in two dimensions

Just as with advection, the process for discretizing the diffusion operators effectively consists of repeating the one-dimensional process for \(x\) in a second dimension \(y\), separately:

\[\kappa \left( \frac{\partial^{2} T}{\partial x^{2}} + \frac{\partial^{2} T}{\partial y^{2}} \right) = \kappa \left( \frac{T_{i+1,\;j}^{n} - 2T_{i,\;j}^{n} + T_{i-1,\;j}^{n}}{\left( \Delta x \right)^{2}} + \frac{T_{i,\;j+1}^{n} - 2T_{i,\;j}^{n} + T_{i,\;j-1}^{n}}{\left( \Delta y \right)^{2}} \right)\]

The corresponding \(x\) and \(y\) second-derivative kernels are shown below:

plt.imshow([[1,1],[0,0],[1,1]], cmap=plt.cm.RdBu_r);
plt.xticks([]);
plt.yticks([0,1,2], labels=[1,-1,1]);

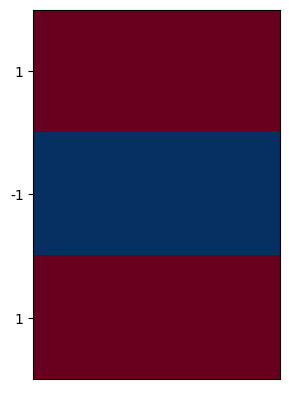
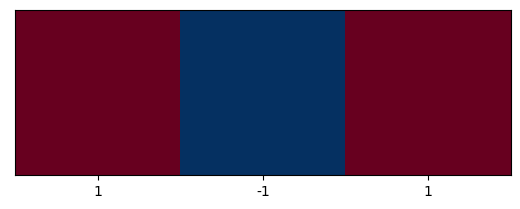
plt.imshow([[1,0,1]], cmap=plt.cm.RdBu_r);
plt.xticks([0,1,2], labels=[1,-1,1]);
plt.yticks([]);

xkernel_diff = np.zeros((1, 3))
xkernel_diff[0, :] = np.array([1,-2,1])

ykernel_diff = np.zeros((3,1))
ykernel_diff[:, 0] = np.array([1,-2,1])

Just as we did with advection, we implement a diffuse function using multiple dispatch:

class OceanModel():
    
    def __init__(self, T, deltat, windfield, grid, kappa):
        
        self.T = [T]
        self.u = windfield.u
        self.v = windfield.v
        self.deltay = grid.deltay
        self.deltax = grid.deltax
        self.deltat = deltat
        self.kappa = kappa
        self.i = np.arange(0, self.T[0].shape[1])
        self.j = np.arange(0, self.T[0].shape[0])
        self.t = [0]
        self.diffuse_out = []
        self.advect_out = []
        self.t_ = []

    def advect(self, T):
        T_advect = np.zeros((self.j.size, self.i.size))
        for j in range(1, T_advect.shape[0] - 1):
            for i in range(1, T_advect.shape[1] - 1):
                T_advect[j, i] = -(self.u[j, i] * np.sum(xkernel[0, :] * T[j, i-1:i+2])/(2*self.deltax) + \
                                   self.v[j, i] * np.sum(ykernel[:, 0] * T[j-1:j+2, i])/(2*self.deltay))
        return T_advect
                
    def diffuse(self, T):
        T_diffuse= np.zeros((self.j.size, self.i.size))
        for j in range(1, T_diffuse.shape[0] - 1):
            for i in range(1, T_diffuse.shape[1] - 1):
                T_diffuse[j, i] = self.kappa*(np.sum(xkernel_diff[0, :] * T[j, i-1:i+2])/(self.deltax**2) + \
                                              np.sum(ykernel_diff[:, 0] * T[j-1:j+2, i])/(self.deltay**2))      
        return T_diffuse

2.3) No-flux boundary conditions

We want to impose the no-flux boundary conditions, which states that

\(u\frac{\partial T}{\partial x} = \kappa \frac{\partial T}{\partial x} = 0\) at \(x\) boundaries and

\(v\frac{\partial T}{\partial y} = \kappa \frac{\partial T}{\partial y} = 0\) at the \(y\) boundaries.

To impose this, we treat \(i=1\) and \(i=N_{x}\) as ghost cells, which do not do anything expect help us impose these boundaries conditions. Discretely, the boundary fluxes between \(i=1\) and \(i=2\) vanish if

\(\dfrac{T_{2,\,j}^{n} -T_{1,\,j}^{n}}{\Delta x} = 0\) or

\(T_{1,\,j}^{n} = T_{2,\,j}^{n}.\)

Thus, we can implement the boundary conditions by updating the temperature of the ghost cells to match their interior-point neighbors:

def update_ghostcells(var):
    var[0, :] = var[1, :];
    var[-1, :] = var[-2, :]
    var[:, 0] = var[:, 1]
    var[:, -1] = var[:, -2]
    return var

B = np.random.rand(6,6)
plt.pcolor(B)
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x13330ee00>

B = update_ghostcells(B)

plt.imshow(B)
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x1333f5660>

2.4) Timestepping

class OceanModel():
    
    def __init__(self, T, deltat, windfield, grid, kappa):
        
        self.T = [T]
        self.u = windfield.u
        self.v = windfield.v
        self.deltay = grid.deltay
        self.deltax = grid.deltax
        self.deltat = deltat
        self.kappa = kappa
        self.i = np.arange(0, self.T[0].shape[1])
        self.j = np.arange(0, self.T[0].shape[0])
        self.t = [0]
        self.diffuse_out = []
        self.advect_out = []
        self.t_ = []

    def advect(self, T):
        T_advect = np.zeros((self.j.size, self.i.size))
        for j in range(1, T_advect.shape[0] - 1):
            for i in range(1, T_advect.shape[1] - 1):
                T_advect[j, i] = -(self.u[j, i] * np.sum(xkernel[0, :] * T[j, i-1:i+2])/(2*self.deltax) + \
                                   self.v[j, i] * np.sum(ykernel[:, 0] * T[j-1:j+2, i])/(2*self.deltax))
        return T_advect
                
    def diffuse(self, T):
        T_diffuse= np.zeros((self.j.size, self.i.size))
        for j in range(1, T_diffuse.shape[0] - 1):
            for i in range(1, T_diffuse.shape[1] - 1):
                T_diffuse[j, i] = self.kappa*(np.sum(xkernel_diff[0, :] * T[j, i-1:i+2])/(self.deltax**2) + \
                                              np.sum(ykernel_diff[:, 0] * T[j-1:j+2, i])/(self.deltay**2))      
        return T_diffuse
    
    def timestep(self):
        T_ = self.T[-1].copy()
        T_ = update_ghostcells(T_)
        tendencies = self.advect(self.T[-1]) + self.diffuse(self.T[-1])
        T_ = self.deltat * tendencies + T_
        self.T.append(T_)
        self.t.append(self.t[-1] + self.deltat)

class grid:   
    """ Creates grid for ocean model
    Args:
    -------
    
    N: Number of grid points (NxN)
    L: Length of domain
    """
    def __init__(self, N, L):
        self.deltax = L / N
        self.deltay = L / N
        self.xs = np.arange(0-self.deltax/2, L+self.deltax/2, self.deltax) 
        self.ys = np.arange(-L-self.deltay/2, L+self.deltay/2, self.deltay)   

        self.N = N
        self.L = L
        self.Nx = len(self.xs)
        self.Ny = len(self.ys)
        self.grid, _= np.meshgrid(self.ys, self.xs, sparse=False, indexing='ij')
        
class windfield:
    """Calculates wind velocity
    
    Args:
    ------
    Grid: class grid()
    option: zero, or single gyre
    
    """
    
    def __init__(self, grid, option = "zero"):
        if option == "zero":
            self.u = np.zeros((grid.grid.shape))
            self.v = np.zeros((grid.grid.shape))
        if option == "single_gyre":
            u, v = PointVortex(grid)
            self.u = u
            self.v = v

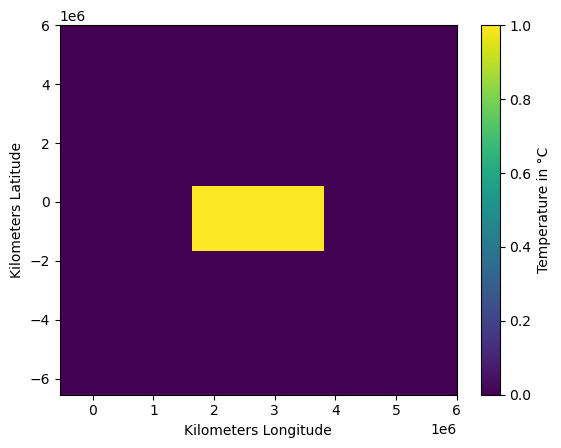
Initialize \(10x10\) grid domain with \(L=6000000m\) and a windfield, where all velocities are set to zero. This should result in diffusion only.

Initialize temperature field with rectangular non-zero box.

my_grid = grid(N = 11, L = 6e6)
my_wind = windfield(my_grid, option = "zero")
my_temp = np.zeros((my_grid.grid.shape)) 
my_temp[9:13, 4:8] = 1

my_grid.grid.shape

(23, 12)

plt.pcolor(my_grid.xs, my_grid.ys, my_temp)
plt.colorbar(label = "Temperature in °C");
plt.ylabel("Kilometers Latitude");
plt.xlabel("Kilometers Longitude");

deltat = 12*60*60 # 12 Hours

def plot_func(steps, temp, deltat, windfield, grid, kappa, anomaly = False):
    my_model = OceanModel(T=temp,
                      deltat=deltat, 
                      windfield=windfield, 
                      grid=grid, 
                      kappa = kappa)
    for step in range(steps):
        my_model.timestep()   
    plt.figure(figsize=(8,8))
    lon, lat = np.meshgrid(grid.xs, grid.ys)
    if anomaly == True:
        plt.pcolor(my_grid.xs, my_grid.ys, my_model.T[-1] - my_model.T[-2], cmap = plt.cm.RdBu_r,
                  vmin = -0.001, vmax = 0.001)
    else:
        plt.pcolor(my_grid.xs, my_grid.ys, my_model.T[-1], vmin = 0, vmax = 1)
    plt.quiver(lon, lat, windfield.u, windfield.v)
    plt.colorbar(label = "Temperature in °C");
    plt.ylabel("Kilometers Latitude");
    plt.xlabel("Kilometers Longitude"); 
    plt.title("Time: {} days".format(int(step/2)))
    plt.show()

interact(plot_func, 
         temp = fixed(my_temp),
         deltat = fixed(deltat),
         windfield = fixed(my_wind),
         grid = fixed(my_grid),
         kappa = fixed(1e4),
         anomaly = widgets.Checkbox(description = "Anomaly", value=False),
         steps = widgets.IntSlider(description="Timesteps", value = 2, min = 1, max = 10000, step = 1));

Create single gyre windfield

def diagnose_velocities(stream, G):    
    dx = np.zeros((G.grid.shape))
    dy = np.zeros((G.grid.shape))
    
    dx = (stream[:, 1:] - stream[:, 0:-1])/G.deltax
    dy = (stream[1:, :] - stream[0:-1, :])/G.deltay
    
    u = np.zeros((G.grid.shape))
    v = np.zeros((G.grid.shape))
    
    u = 0.5*(dy[:, 1:] + dy[:, 0:-1])
    v = -0.5*(dx[1:, :] + dx[0:-1, :])
    
    return u, v

def impose_no_flux(u, v):
    u[0, :]  = 0; v[0, :] = 0;
    u[-1,:]  = 0; v[-1,:] = 0;
    u[:, 0]  = 0; v[:, 0] = 0;
    u[:,-1]  = 0; v[:,-1] = 0;
    
    return u, v

def PointVortex(G, omega = 0.6, a = 0.2, x0=0.5, y0 = 0.):
    x = np.arange(-G.deltax/G.L, 1 + G.deltax / G.L, G.deltax / G.L).reshape(1, -1)
    y = np.arange(-1-G.deltay/G.L, 1+ G.deltay / G.L, G.deltay / G.L).reshape(-1, 1)
        
    r = np.sqrt((y - y0)**2 + (x - x0)**2)
    stream = -omega/4*r**2 
    stream[r > a] =  -omega*a**2/4*(1. + 2*np.log(r[r > a]/a))
    
    u, v =  diagnose_velocities(stream, G)
    u, v = impose_no_flux(u, v) 
    u = u * G.L; v = v * G.L
    return u, v

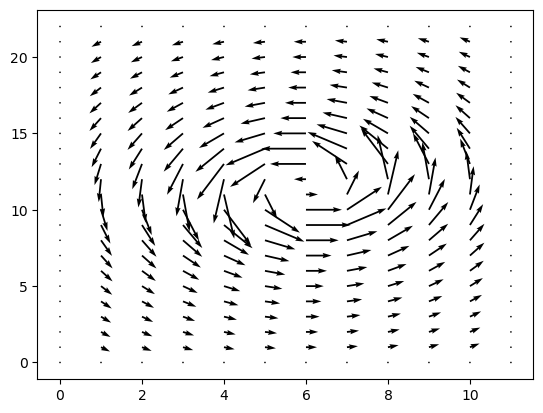
my_wind = windfield(my_grid, option="single_gyre")
plt.quiver(my_wind.u, my_wind.v)

<matplotlib.quiver.Quiver at 0x134f329b0>

my_temp = np.zeros((my_grid.grid.shape)) 
my_temp[8:13, :] = 1

plt.pcolor(my_temp)

<matplotlib.collections.PolyCollection at 0x134f30190>

my_model = OceanModel(T=my_temp,
                      deltat=deltat, 
                      windfield=my_wind, 
                      grid=my_grid, 
                      kappa = 1e4)

interact(plot_func, 
         temp = fixed(my_temp),
         deltat = fixed(deltat),
         windfield = fixed(my_wind),
         grid = fixed(my_grid),
         kappa = widgets.IntSlider(description="kappa", value = 1e4, min=1e3, max = 1e5, step = 100),
         anomaly = widgets.Checkbox(description = "Anomaly", value=False),
         steps = widgets.IntSlider(description="Timesteps", value = 1, min = 1, max = 1000, step = 1));

Optional: Create two gyres!